EXAM 3 (TAKE HOME): (Print and answer in the space provided. Staple and Submit. Due in-class on April 25th at 1 PM).
Quizzes 4-6 posted.
Quiz 7 Reading List: (In-class Quiz on April 18th; CLOSED NOTES).
Projects 1-8 posted.
—————————————————–
Dr. Meg's Desktop Selected Lecture Videos
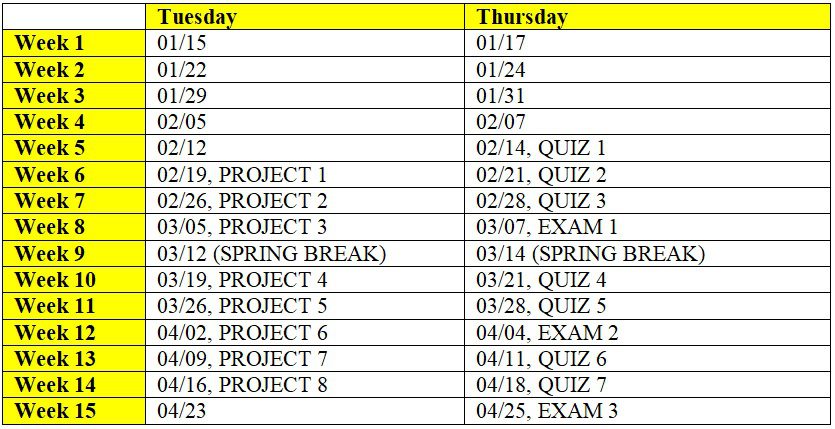
Quiz, Exam and Project Schedules
—————————————————–
Syllabus
Teaching Assistant
Lecture Slides
Module 1: Algorithm Efficiency Analysis (Last Updated: Jan. 31st)
Module 2: Divide and Conquer (Last Updated: Feb. 6th)
Module 4: Dynamic Programming (Last Updated: March 5th)
Module 5: Graph Algorithms (Last Updated: April 2nd)
Module 6: P, NP, NP-Complete Problems
Question Bank
QB Module 1: Algorithm Efficiency Analysis
QB Module 2 – Classical Design Techniques
QB Module 4 – Dynamic Programming
QB Module 5 – Graph Theory Algorithms
Project Descriptions
Project 1: Brute Force Algorithm for the Element Uniqueness Problem (Due: Feb. 19th, 1 PM)
Project 2: Implementation and Performance Comparison of the Bubble Sort and Insertion Sort Algorithms (Due: Feb. 26th, 11.59 PM)
Project 4: Binary Search vs. Brute Force Search Algorithms for Finding a Local Minimum in a Two-Dimensional Array (Due: March 19th, by 11.59 PM)
Project 5: Dynamic Programming Algorithm for Optimum Coin Collection in a Two-Dimensional Grid (Due: March 26th, by 11.59 PM)
Project 6: Dynamic Programming-based Solution for the Longest Common Subsequence Problem (Due: April 2nd, by 11.59 PM)
Project 7: Dynamic Programming: Coin Change Problem (Due: April 9th, by 11.59 PM)
Project 8: Number of Walks of a certain Length between any Two Vertices (Due: April 16th, by 11.59 PM)
Quizzes and Exams
Quiz 2 (Due: Feb. 21st, 1 PM)
Exam 1 (Take Home): Due by March 7th, 1 PM
Quiz 4 (Programming): Implementation of the Greedy Algorithm to Determine an Optimal Allocation of Files in a Tape to Minimize the Average Cost to Access the Files (Due: March 21st, by 11.59 PM)
Quiz 5 (No Programming; Take Home): Matrix Chain Multiplication (Due: March 28th, by 1 PM)
Quiz 6 (No Programming; Take Home): Prim's Minimum Spanning Tree Algorithm (Due: April 11th, by 1 PM)
Exam 2 (Take Home): Due by April 4th, 1 PM
EXAM 3 (TAKE HOME): (Print and answer in the space provided. Staple and Submit. Due in-class on April 25th at 1 PM).
Code Tutorial
Dr. Meg's Desktop Selected Lecture Videos (YouTube Links)
Module 1: Analyzing the Efficiency of Algorithms
Time-Complexity analysis of a recursive algorithm to compute the factorial of an integer
Example for solving recurrence relations
Time-complexity analysis of an iterative algorithm to determine whether an array has unique elements
Decrease and Conquer – Insertion Sort Algorithm and Examples
Module 2: Classical Algorithm Design Techniuqes
Brute Force Algorithms QB – String Matching Problems
Divide and Conquer – Theorem-Proof: In order Traversal of a Binary Search Tree
Divide and Conquer – Master Theorem
Binary Search Algorithm and Examples
Comparison of Bottom-up and Top-down Approaches for Heap Construction
Transform and Conquer – Proof for Euclid's GCD Formula
Transform and Conquer – Heap Sort
Space-Time Tradeoffs for the Sorting Algorithms (Merge, Insertion and Heap Sorts)
Module 3: Greedy Technique
Greedy Technique – Fractional Knapsack Problem
Greedy Technique – Huffman Codes (Variable Length Prefix-free Encoding)
Module 4: Dynamic Programming
Dynamic Programming: Coin-row Problem Discussion and Example
Dynamic Programming: Binomial Coefficient
Dynamic Programming Solution for the Coin Collecting Problem in a Two-Dimensional Grid
Dynamic Programming: Integer Knapsack Problem (0-1 Knapsack Problem)
Module 5: Graph Theory Algorithms
Depth First Search on Directed Graph
Depth First Search and Articulation Points
Breadth First Search and 2-Colorability of Graphs
Topological Sort on DAGs and Proof for Neccessary and Sufficient Condition
Dijkstra's Algorithm for Shortest Path Trees and Proof for Correctness
Bellman-Ford Algorithm for Shortest Path Trees and Examples New!!
Kruskal's Algorithm: Examples to find Minimum Spanning Trees
Kruskal's Algorithm: Proof of Correctness
Properties (1 and 2) of Minimum Spanning Tree: IJ-Cut and Minimum Weight Edge
Prim's Algorithm for Minimum Spanning Trees and Proof for Correctness
Floyd's All Pairs Shortest Paths Algorithm
Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7
Module 6: P, NP and NP-Complete Problems
Polynomial Reduction: Hamiltonian Circuit to Traveling Salesman Problem
Polynomial Reductions: Independent Set, Clique and Vertex Cover
Multi-fragment Heuristic for the Traveling Salesman Problem