CSC 323 Algorithm Design and Analysis, Fall 2020

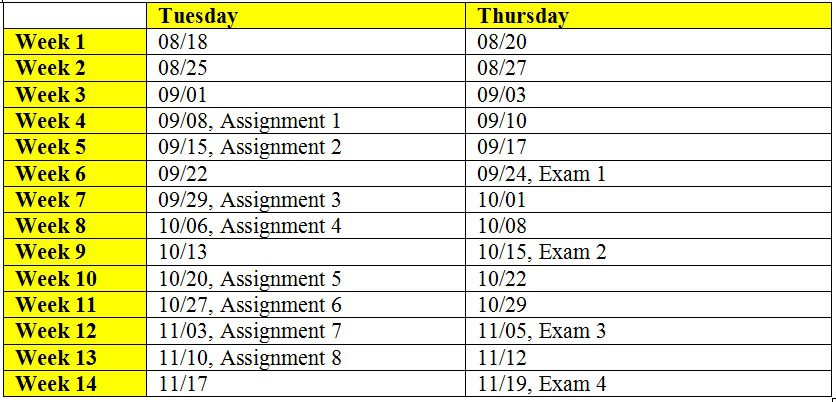
Assignments 1, 2 and Exam 1 posted.

 

---

Syllabus

CSC323 Syllabus, Fall 2020

 

Teaching Assistants (TAs)

Landrie Tchakoua
Zoom (Meeting ID: 816 538 7125)
Tuesday 10 AM to 12 PM
Wednesday 12 PM to 4 PM
Thursday 10 AM to 12 PM; 4 PM to 6 PM


Oluwaseun Akintade
Google Meet Link: https://meet.google.com/jqv-druy-njz (Links to an external site.)
Monday 12 PM to 6 PM
Wednesday 11 AM to 3 PM
Friday 1 PM to 5 PM

 

Lecture Slides

Module 1: Algorithm Efficiency Analysis

Module 2: Divide and Conquer

Module 3: Binary Search

Module 4: Greedy Strategy

Module 5: Dynamic Programming

Sample C++ Code and Explanation on dynamically creating and using a two-dimensional array

Module 6: Graph Algorithms

Module 7: P, NP, NP-Complete Problems

 

Question Bank

Algorithm Efficiency Analysis

Classical Design Techniques (includes Divide and Conquer, Binary Search)

Greedy Strategy

Dynamic Programming

Graph Theory Algorithms

Assignments

Assignment 1: Brute Force Algorithm for the Element Uniqueness Problem, Due: Sept. 8th, 11.59 PM

Assignment 2: Algorithm to Determine the Longest Subsequence of Consecutive Integers in an Array using Hash tables, its Optimization and the Analysis of the Space-Time Tradeoff, Due: Sept. 15th, 2020, by 11.59 PM

Check Canvas for Code

 

 

Exams

Exam 1 (covers Modules 1 and 2); Due by Sept. 24th, 11.59 PM

 

 

 

Dr. Meg’s Desktop Selected Lecture Videos (YouTube Links)

Analyzing the Efficiency of Algorithms

Time-Complexity analysis of a recursive algorithm to compute the factorial of an integer

Example for solving recurrence relations

Time-complexity analysis of an iterative algorithm to determine whether an array has unique elements

Time-Complexity analysis of a recursive algorithm to determine the number of bits needed to represent a positive integer

Decrease and Conquer – Insertion Sort Algorithm and Examples

Classical Algorithm Design Techniuqes

Brute Force Algorithms QB – String Matching Problems

Divide and Conquer – Theorem-Proof: In order Traversal of a Binary Search Tree

Divide and Conquer – Master Theorem

Binary Search Algorithm and Examples

Comparison of Bottom-up and Top-down Approaches for Heap Construction

Transform and Conquer – Proof for Euclid’s GCD Formula

Transform and Conquer – Heap Sort

Space-Time Tradeoffs for the Sorting Algorithms (Merge, Insertion and Heap Sorts)

Greedy Technique

Greedy Technique – Fractional Knapsack Problem

Greedy Technique – Huffman Codes (Variable Length Prefix-free Encoding)

Dynamic Programming

Dynamic Programming: Coin-row Problem Discussion and Example

Dynamic Programming: Binomial Coefficient

Dynamic Programming Solution for the Coin Collecting Problem in a Two-Dimensional Grid

Dynamic Programming: Integer Knapsack Problem (0-1 Knapsack Problem)

Graph Theory Algorithms

Depth First Search on Directed Graph

Depth First Search and Articulation Points

Breadth First Search and 2-Colorability of Graphs

Topological Sort on DAGs and Proof for Neccessary and Sufficient Condition

Dijkstra’s Algorithm for Shortest Path Trees and Proof for Correctness

Bellman-Ford Algorithm for Shortest Path Trees and Examples New!!

Kruskal’s Algorithm: Examples to find Minimum Spanning Trees

Kruskal’s Algorithm: Proof of Correctness

Properties (1 and 2) of Minimum Spanning Tree: IJ-Cut and Minimum Weight Edge

Properties (3 and 4) of Minimum Spanning Tree: A graph with unique edge weights has only one minimum spanning tree

Property 5 of Minimum Spanning Tree: Given a graph with unique edge weights, the largest weight edge in any cycle cannot be part of any minimum spanning tree

Prim’s Algorithm for Minimum Spanning Trees and Proof for Correctness

Floyd’s All Pairs Shortest Paths Algorithm

Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7

P, NP and NP-Complete Problems

Polynomial Reduction: Hamiltonian Circuit to Traveling Salesman Problem

Minimal Number of Uncovered Neighbors Heuristic: Example to determine an Independent Set, Vertex Cover and Clique

Polynomial Reductions: Independent Set, Clique and Vertex Cover

Multi-fragment Heuristic for the Traveling Salesman Problem

Twice around the tree Heuristic for the Traveling Salesman Problem and the Proof for approximation ratio

 

 

 

Assignment and Exam Schedules