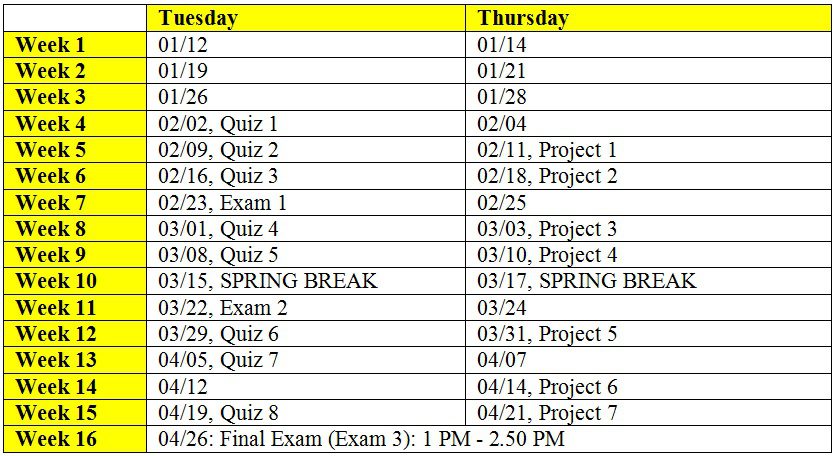
Quiz 8 on April 19th: (Theorem Proving Quiz): CLOSED NOTES. Reading List
Exam 3 (Final Exam) on April 26th: 1 PM to 2.50 PM. OPEN NOTES. Reading List
Projects 6 and 7 posted.
—————————————————–
Syllabus
Lecture Slides
Question Bank
Project Descriptions
Quiz Solutions
Dr. Meg's Desktop Selected Lecture Videos
Quiz, Exam and Project Schedules
—————————————————–
Syllabus
Lecture Slides
Module 1: Algorithm Efficiency Analysis
Module 2: Classical Design Techniques
Module 6: NP-Complete Problems and Heuristics
Question Bank
QB Module 1: Algorithm Efficiency Analysis
QB Module 2 – Classical Design Techniques
QB Module 4 – Dynamic Programming
QB Module 5 – Graph Theory Algorithms
Project Descriptions
Project 1: Element Uniqueness Problem, Due: Feb. 11
Project 2: Iterative vs. Recursive Algorithms to Compute the Factorial of an Integer, Due: Feb. 18
Project 3: Computing h-index using Sorting and Max-Min Formulation, Due: March 3
Project 4: Determining the Maximum Element in an Unimodal Array using the Binary Search Logic, Due: March 10
Project 5: Determining the Common Elements across All Arrays using Hash Tables and Java Collection Classes, Due: March 31
Project 6: Bloom Filter and Breadth First Search, Due: April 14, 2016
Project 7: Maximum Bottleneck Path Problem, Due: April 21, 2016
Quiz Solutions
Dr. Meg's Desktop Selected Lecture Videos (YouTube Links)
Module 1 (Chapter 2): Analyzing the Efficiency of Algorithms
Time-Complexity analysis of a recursive algorithm to compute the factorial of an integer
Example for solving recurrence relations
Time-complexity analysis of an iterative algorithm to determine whether an array has unique elements
Module 2 (Chapters 3-6): Classical Algorithm Design Techniuqes
Brute Force Algorithms QB – String Matching Problems
Decrease and Conquer – Insertion Sort Algorithm and Examples
Divide and Conquer – Theorem-Proof: In order Traversal of a Binary Search Tree
Divide and Conquer – Master Theorem
Binary Search Algorithm and Examples
Comparison of Bottom-up and Top-down Approaches for Heap Construction
Transform and Conquer – Proof for Euclid's GCD Formula
Transform and Conquer – Heap Sort
Space-Time Tradeoffs for the Sorting Algorithms (Merge, Insertion and Heap Sorts)
Module 3 (Chapter 9): Greedy Technique
Greedy Technique – Fractional Knapsack Problem
Greedy Technique – Huffman Codes (Variable Length Prefix-free Encoding)
Module 4 (Chapter 8): Dynamic Programming
Dynamic Programming: Coin-row Problem Discussion and Example
Dynamic Programming: Binomial Coefficient
Dynamic Programming Solution for the Coin Collecting Problem in a Two-Dimensional Grid
Dynamic Programming: Integer Knapsack Problem (0-1 Knapsack Problem)
Module 5: Graph Theory Algorithms
Depth First Search on Directed Graph
Depth First Search and Articulation Points
Breadth First Search and 2-Colorability of Graphs
Topological Sort on DAGs and Proof for Neccessary and Sufficient Condition
Dijkstra's Algorithm for Shortest Path Trees and Proof for Correctness
Bellman-Ford Algorithm for Shortest Path Trees and Examples New!!
Kruskal's Algorithm: Examples to find Minimum Spanning Trees
Kruskal's Algorithm: Proof of Correctness
Properties (1 and 2) of Minimum Spanning Tree: IJ-Cut and Minimum Weight Edge
Prim's Algorithm for Minimum Spanning Trees and Proof for Correctness
Floyd's All Pairs Shortest Paths Algorithm
Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7
Module 6: P, NP and NP-Complete Problems
Polynomial Reduction: Hamiltonian Circuit to Traveling Salesman Problem
Polynomial Reductions: Independent Set, Clique and Vertex Cover
Multi-fragment Heuristic for the Traveling Salesman Problem
Quiz, Exam and Project Schedules