CSC 323 Algorithm Design and Analysis, Spring 2020 - Natarajan Meghanathan, Professor of Computer Science, Jackson State University

Assignment 12 (Due: 04/21, by 11.59 PM) posted.

Assignment 13: Quiz (Due: 04/23, by 11.59 PM) posted in Canvas.

Reading List of Topics for Assignment 13 (Quiz to be posted in Canvas; will be due on 04/23, by 11.59 PM)

Take Home Exam 4 posted (also available in Canvas). Due in Canvas by April 28th, 11.59 PM for both graduating and non-graduating students.

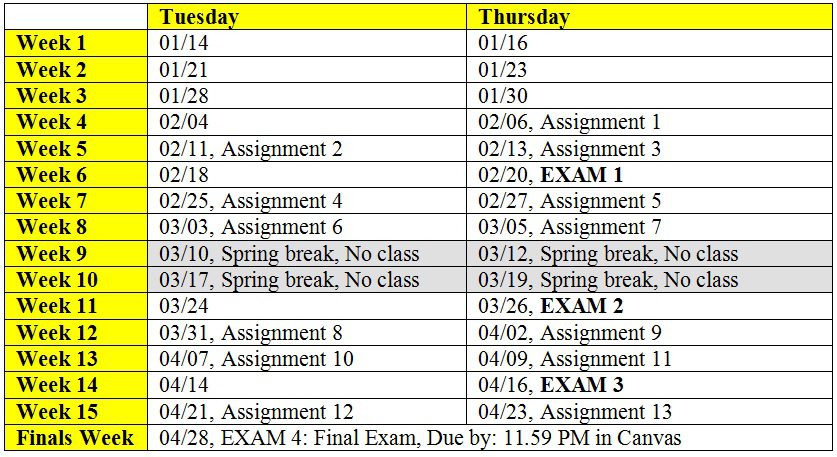
Check Assignment and Exam Schedules for the updated schedule of the course

—————————————————–

Dr. Meg's Desktop Selected Lecture Videos

Assignment and Exam Schedules

—————————————————–

Syllabus

CSC323 Syllabus, Spring 2020

Teaching Assistant (TA)

Amanuel Gebre: Mondays, Fridays: 10 AM to 3 PM; Wednesdays: 11 AM to 3 PM

Office Hours in Canvas: Meet the TA using the "Chat" feature in Canvas during the above timings

E-mail: J00801049@students.jsums.edu

Check Canvas for the timer code.

Assignment 4 (Programming): Design and Implementation of a Θ(n) Algorithm to Determine the Most Frequently Occurring Integer in an Array of Integers

Check Canvas for the code.

Assignment 5 (Programming): Comparison of two Recursive Algorithms to Determine the Minimum Element in an Array

Check Canvas for the code.

Assignment 6 (Programming): Using the Merge Sort Algorithm to Determine the Number of Inversions and the Inverted Pairs of an Array

Check Canvas for the code.

Assignment 7 (Programming): Binary Search vs. Brute Force Search Algorithms for Finding a Local Minimum in a Two-Dimensional Array

Assignment 8 (Programming): Dynamic Programming Algorithm for Optimum Coin Collection in a Two-Dimensional Grid

Check Canvas for the sample C++ code to work with two-dimensional arrays.

Assignment 9 (Programming): Dynamic Programming-based Solution for the Longest Common Subsequence Problem

Assignment 10 (Programming): Dynamic Programming: Coin Change Problem

Check Canvas for the Code

Assignment 11 (Non-Programming-Take Home): Matrix Chain Multiplication (Submit a word or PDF version of the solutions in Canvas by April 9th, 11.59 PM.)

Assignment 12 (Non-Programming-Take Home): Prim's Minimum Spanning Tree Algorithm (Submit a PDF version of the solutions in Canvas by April 21st, 11.59 PM.)

Exams

Take Home Exam 2 (also available in Canvas). Due in Canvas by March 26th, 11.59 PM.

Take Home Exam 3 posted (also available in Canvas). Due in Canvas by April 16th, 11.59 PM.

Take Home Exam 4 posted (also available in Canvas). Due in Canvas by April 28th, 11.59 PM. For Graduating seniors, it is due on April 24th, 11.59 PM

Dr. Meg's Desktop Selected Lecture Videos (YouTube Links)

Module 1: Analyzing the Efficiency of Algorithms

Time-Complexity analysis of a recursive algorithm to compute the factorial of an integer

Example for solving recurrence relations

Time-complexity analysis of an iterative algorithm to determine whether an array has unique elements

Time-Complexity analysis of a recursive algorithm to determine the number of bits needed to represent a positive integer

Decrease and Conquer – Insertion Sort Algorithm and Examples

Module 2: Classical Algorithm Design Techniuqes

Brute Force Algorithms QB – String Matching Problems

Divide and Conquer – Theorem-Proof: In order Traversal of a Binary Search Tree

Divide and Conquer – Master Theorem

Binary Search Algorithm and Examples

Comparison of Bottom-up and Top-down Approaches for Heap Construction

Transform and Conquer – Proof for Euclid's GCD Formula

Transform and Conquer – Heap Sort

Space-Time Tradeoffs for the Sorting Algorithms (Merge, Insertion and Heap Sorts)

Module 3: Greedy Technique

Greedy Technique – Fractional Knapsack Problem

Greedy Technique – Huffman Codes (Variable Length Prefix-free Encoding)

Module 4: Dynamic Programming

Dynamic Programming: Coin-row Problem Discussion and Example

Dynamic Programming: Binomial Coefficient

Dynamic Programming Solution for the Coin Collecting Problem in a Two-Dimensional Grid

Dynamic Programming: Integer Knapsack Problem (0-1 Knapsack Problem)

Module 5: Graph Theory Algorithms

Depth First Search on Directed Graph

Depth First Search and Articulation Points

Breadth First Search and 2-Colorability of Graphs

Topological Sort on DAGs and Proof for Neccessary and Sufficient Condition

Dijkstra's Algorithm for Shortest Path Trees and Proof for Correctness

Bellman-Ford Algorithm for Shortest Path Trees and Examples New!!

Kruskal's Algorithm: Examples to find Minimum Spanning Trees

Kruskal's Algorithm: Proof of Correctness

Properties (1 and 2) of Minimum Spanning Tree: IJ-Cut and Minimum Weight Edge

Properties (3 and 4) of Minimum Spanning Tree: A graph with unique edge weights has only one minimum spanning tree

Property 5 of Minimum Spanning Tree: Given a graph with unique edge weights, the largest weight edge in any cycle cannot be part of any minimum spanning tree

Prim's Algorithm for Minimum Spanning Trees and Proof for Correctness

Floyd's All Pairs Shortest Paths Algorithm

Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7

Module 6: P, NP and NP-Complete Problems

Polynomial Reduction: Hamiltonian Circuit to Traveling Salesman Problem

Minimal Number of Uncovered Neighbors Heuristic: Example to determine an Independent Set, Vertex Cover and Clique

Polynomial Reductions: Independent Set, Clique and Vertex Cover

Multi-fragment Heuristic for the Traveling Salesman Problem

Twice around the tree Heuristic for the Traveling Salesman Problem and the Proof for approximation ratio